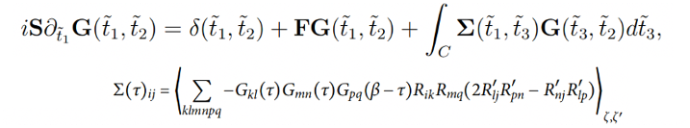Our research of interests lies in theoretical/physical chemistry, with a special focus on
nonadiabatic (quantum) dynamics and (excited states) electronic structure theory for molecular
systems in condensed phase, at interfaces, and within nanomaterials . To be more specific,
Nonadiabatic dynamics:
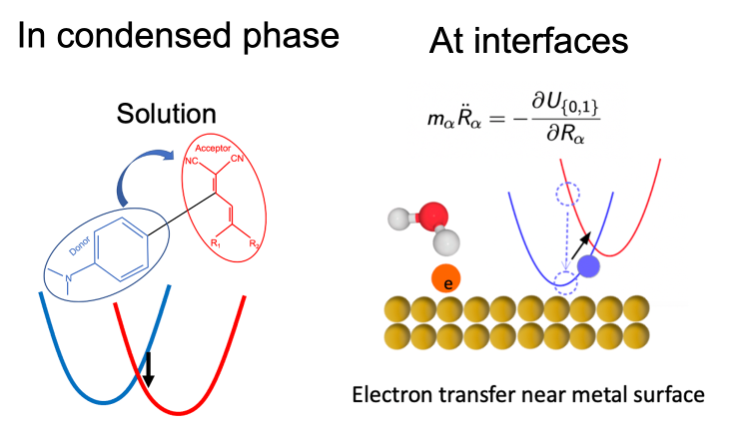
We are interested in nonadiabatic dynamics in condensed phase or at interfaces, where we have
developed and implemented surface hopping and electronic friction approaches to study electron and energy
transfer at molecule-metal interfaces. Such studies are very relevant to many chemical systems, e.g.
electrochemistry, chemisorption, nanojunctions. we have derived classical master equation and generalized
Langevin equation to describe coupled electron-nuclear motion near metal surfaces. The nonadiabatic
electron transfer processes at molecule-metal interfaces are either being incorporated into stochastic
hopping events between different potential energy surfaces (classical master equation/surface hopping)
or being incorporated into frictional effects (generalized Langevin equation/electronic friction).
We have derived a general framework to calculate electronic friction both in equilibrium and out of
equilibrium. When electronic correlations are included, we find that frictional coefficients exhibit
Kondo features. Such a framework also provides a general treatment to quantum thermodynamics on open
quantum system.
Reference:
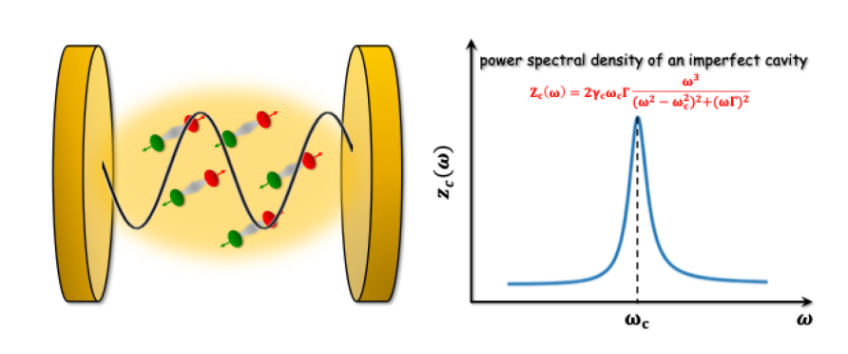
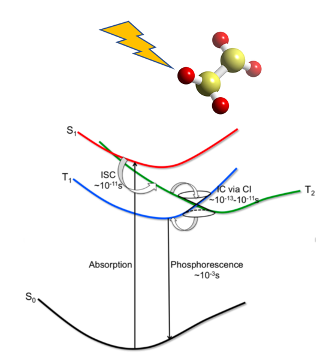
Strong light-matter interactions:
Light can modify chemical reactions and nonadiabatic electron transfer processes strenuously, particularly when
we have strong light-matter interactions. In the case of strong light-matter interactions, the traditional perturbation
theory fails. We develop new dynamical methods for treating strong light-matter interactions at metal surfaces as well as
inside an optical cavity. Such a scenario is very relevant to photoelectrochemistry, photo-catalysis, and molecular
polaritonic chemistry. In the case of strong vibrational couplings, we derive a Langevin equation, where cavity
induced friction can enhance and suppress the rate processes. In the case of electronic strong couplings,
we arrive at a Floquet surface hopping and Floquet electronic friction approaches. We also formulate a
Marcus-like nonadiabatic electron transfer rate. We find that the electron transfer rate shows a turnover as
a function of the driving frequency of light.
Reference:
1. J. P. Philbin,
Y. Wang, P. Narang,
W. Dou.
"Chemical reactions in imperfect cavities: enhancement, suppression, and resonance".
J. Phys. Chem. C (2022).
Download
Electron and spin transport in nanomaterials:
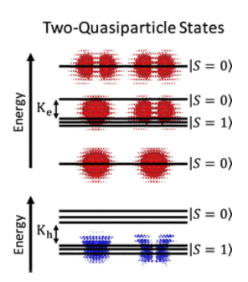
Semiconductor quantum dots (QDs) have been studied and utilized for a wide range of applications,
including light-emitting diodes, lasers, photocatalysis, nanojunctions, and quantum information processing.
All of these applications require a detailed understanding of the excited states in these confined
semiconductors. we combine atomistic electronic structure calculations with quantum master equation
methods to study the transport of electrons and holes through strongly confined quantum dots coupled
to two leads with a voltage bias. We find that a competition between the energy spacing between the
two lowest quasi-particle energy levels and the strength of the exchange interaction determines the spin
states of the lowest two quasi-particle energy levels. The exchange interaction is also responsible for
spin blockades in transport properties.
Reference:
Excited-state electronic structure theory :
The group also investigates the efforts to effectively calculate the excited-state electronic structure theory
for molecules and extended systems. We are developing the cutting edged tools to treat many-electron problems,
with a special focus on the many-body perturbation theory and Green's functions, e.g.
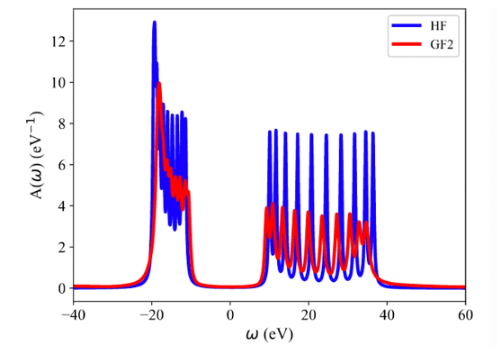
GW, Bethe-Salpeter equation, second-order Green's function (GF2 or MP2). In these methods,
the electronic correlations are incorporated into the self-energy, which is very inefficiently to
evaluate due to high computational cost. The computational scaling of such step is O(N^5) or more, which
limits the application of these methods to relatively small system size (say, 100 electrons). To overcome the
computational bottleneck, we have introduced the stochastic implementation of these methods, called the stochastic
resolution of identity approach, which greatly reduce the computational cost down to O(N^3). As tested on molecular
and extended systems (e.g. Hydrogen molecule chain) GF2 predicts quasi-particle properties better than Hartree-Fock (HF)
and density functional theory (DFT), and has a similar accuracy as GW method.
Reference:
1.
W. Dou, T.Y. Takeshita, M. Chen, R. Baer, D. Neuhauser, E. Rabani.“Stochastic Resolution
of Identity for Real-Time Second-Order Green’s Function: Ionization Potential and Quasi-particle Spectrum”.
J. Chem. Theory Comput.15, 6703 (2019).
Download
2. T.Y. Takeshita,
W. Dou, D.G.A. Smith, W.A. de Jong, R. Baer, D. Neuhauser, E. Rabani.
“Stochastic resolution of identity second-order Matsubara Green’s function theory”.
J. Chem. Phys.151, 044114 (2019).
Download
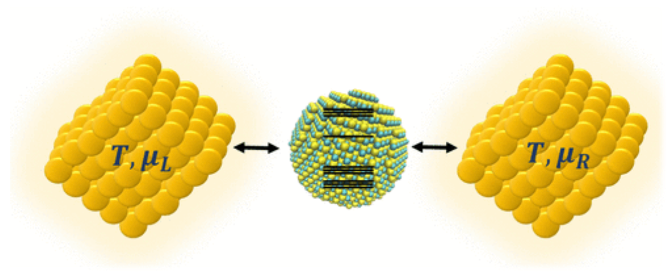
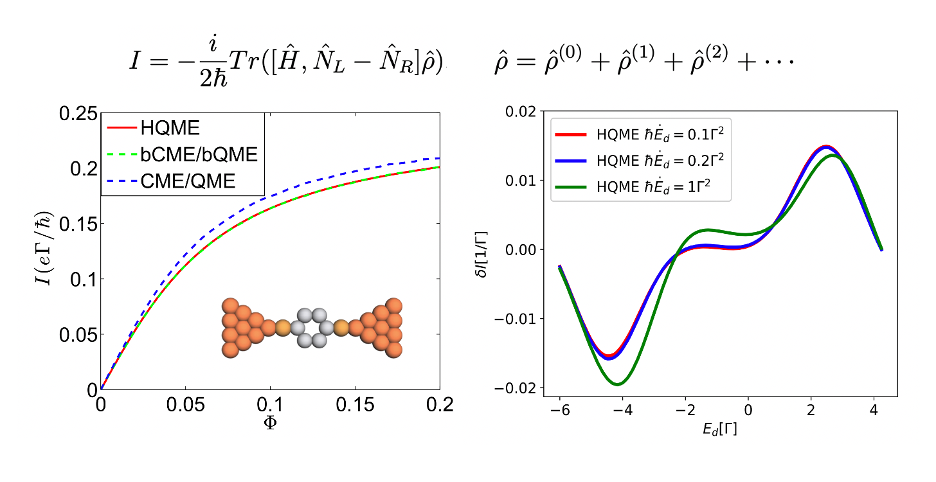
Nonequilibrium quantum dynamics:
We also develop new methods to treat quantum dynamics at non-equilibrium conditions, i.e. under driving,
carrying on an electron or heat current throughout the system. One of such quantum systems are nano-junctions,
where a quantum dot or a molecular system coupled with two leads. We study entropy production and electron-phonon
couplings throughout the transport properties, i.e. current-voltage curves, heat flows, and energy conversion.
One of such method is based on response theory, where we capture non-adiabatic correction to the thermodynamic
quantities with external driving, and we manifest the first and second thermodynamic law in the quantum regimes.
Reference:
1.
W. Dou, C. Schinabeck, M. Thoss, J.E. Subotnik.“A broadened
classical master equation approach for treating electron-nuclear coupling in non-equilibrium transport”
J. Chem. Phys.148, 102317 (2018).
Download
2.
W. Dou, J. Bätge, A. Levy, M. Thoss.
Universal approach to quantum thermodynamics of strongly coupled systems under nonequilibrium conditions and external driving.
Phys.Rev.B101, 184304 (2020).
Download